Hierarchical regression comes down to comparing different regression models. Each model adds 1(+) predictors to the previous model, resulting in a “hierarchy” of models. This analysis is easy in SPSS but we should pay attention to some regression assumptions:
- linearity: each predictor has a linear relation with our outcome variable;
- normality: the prediction errors are normally distributed in the population;
- homoscedasticity: the variance of the errors is constant in the population.
Also, let's ensure our data make sense in the first place and choose which predictors we'll include in our model. The roadmap below summarizes these steps.
SPSS Hierarchical Regression Roadmap
| Step | Why? | Action? | |
|---|---|---|---|
| 1 | Inspect histograms | See if distributions make sense. | Set missing values. Exclude variables. |
| 2 | Inspect descriptives | See if any variables have low N. Inspect listwise valid N. | Exclude variables with low N. |
| 3 | Inspect scatterplots | See if relations are linear. Look for influential cases. | Exclude cases if needed. Transform predictors if needed. |
| 4 | Inspect correlation matrix | See if Pearson correlations make sense. | Inspect variables with unusual correlations. |
| 5 | Regression I: model selection | See which model is good. | Exclude variables from model. |
| 6 | Regression II: residuals | Inspect residual plots. | Transform variables if needed. |
Case Study - Employee Satisfaction
A company held an employee satisfaction survey which included overall employee satisfaction. Employees also rated some main job quality aspects, resulting in work.sav.
The main question we'd like to answer is which quality aspects predict job satisfaction? Let's follow our roadmap and find out.
Inspect All Histograms
Let's first see if our data make any sense in the first place. We'll do so by running histograms over all predictors and the dependent variable. The easiest way for doing so is running the syntax below. For more detailed instructions, see Creating Histograms in SPSS.
frequencies overall to tasks
/format notable
/histogram.
Result
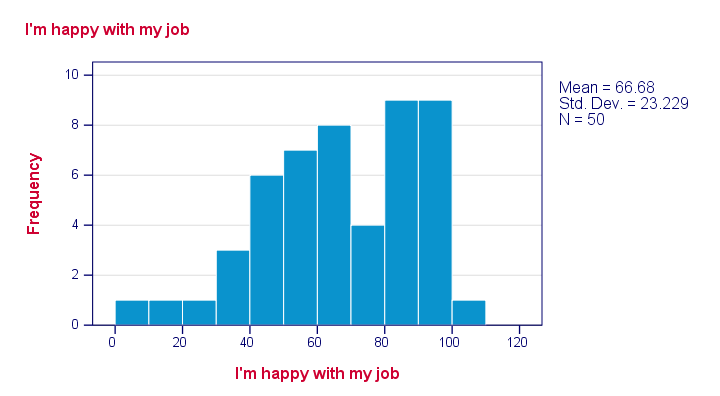
Just a quick look at our 6 histograms tells us that
- none of these variables contain any system missing values;
- none of our variables contain any clear outliers: there's no need to set any user missing values;
- all frequency distributions look plausible.
If histograms do show unlikely values, it's essential to set those as user missing values before proceeding with your analyses.
Inspect Descriptives Table
If variables contain missing values, a simple descriptives table is a fast way to inspect the extent of missingness. We'll run it from a single line of syntax .
descriptives overall to tasks.
Result
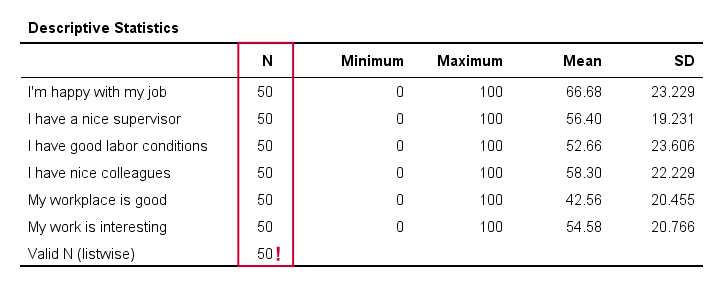
The descriptives table tells us if any variables have many missing values. If so, you may want to exclude such variables from analysis.
Valid N (listwise) is the number of cases without missing values on any variables in this table. SPSS regression (as well as factor analysis) uses only such complete cases unless you select pairwise deletion of missing values as we'll see in a minute.
Inspect Scatterplots
Do our predictors have (roughly) linear relations with the outcome variable? Most textbooks suggest inspecting residual plots: scatterplots of the predicted values (x-axis) with the residuals (y-axis) are supposed to detect non linearity.
However, I think residual plots are useless for inspecting linearity. The reason is that predicted values are (weighted) combinations of predictors. So what if just one predictor has a curvilinear relation with the outcome variable? This curvilinearity will be diluted by combining predictors into one variable -the predicted values.
It makes much more sense to inspect linearity for each predictor separately. A minimal way to do so is running scatterplots for each predictor (x-axis) with the outcome variable (y-axis).
A simple way to create these scatterplots is to just one command from the menu as shown in SPSS Scatterplot Tutorial. Next, remove the line breaks and copy-paste-edit it as needed.
GRAPH /SCATTERPLOT(BIVAR)= supervisor WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= conditions WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= colleagues WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= workplace WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= tasks WITH overall /MISSING=LISTWISE.
Result
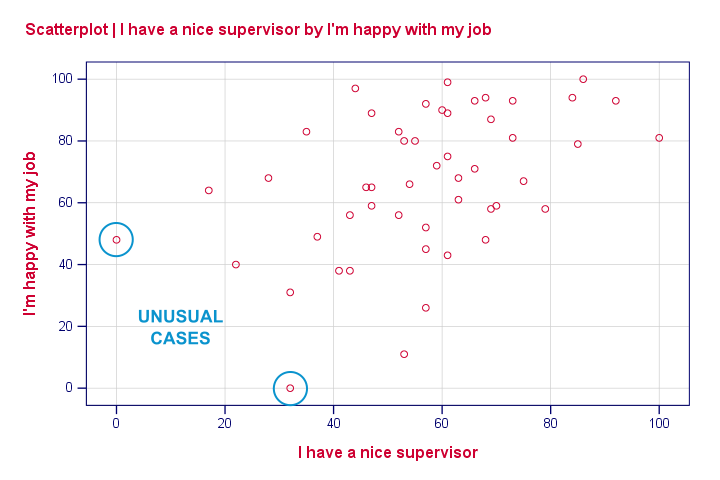
None of our scatterplots show clear curvilinearity. However, we do see some unusual cases that don't quite fit the overall pattern of dots. We'll flag and inspect these cases with the syntax below.
compute flag1 = (overall > 40 and supervisor < 10).
*Move unusual case(s) to top of file for visual inspection.
sort cases by flag1(d).
Result
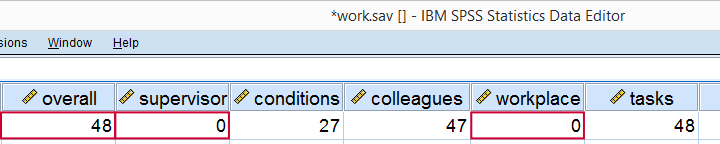
Our first case looks odd indeed: supervisor and workplace are 0 -couldn't be worse- but overall job rating is quite good. We should perhaps exclude such cases from further analyses with FILTER but we'll just ignore them for now.
Regarding linearity, our scatterplots provide a minimal check. A much better approach is inspecting linear and nonlinear fit lines as discussed in How to Draw a Regression Line in SPSS?
An excellent tool for doing this super fast and easy is downloadable from SPSS - Create All Scatterplots Tool.
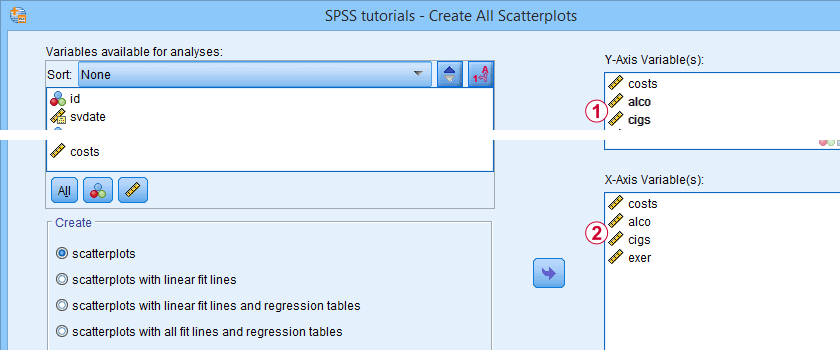
Inspect Correlation Matrix
We'll now see if the (Pearson) correlations among all variables make sense. For the data at hand, I'd expect only positive correlations between, say, 0.3 and 0.7 or so. For more details, read up on SPSS Correlation Analysis.
correlations overall to tasks
/print nosig
/missing pairwise.
Result
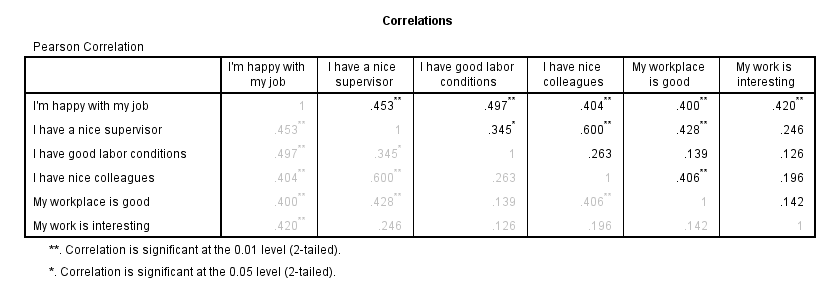
The pattern of correlations looks perfectly plausible. Creating a nice and clean correlation matrix like this is covered in SPSS Correlations in APA Format.
Regression I - Model Selection
The next question we'd like to answer is:
which predictors contribute substantially
to predicting job satisfaction?
Our correlations show that all predictors correlate statistically significantly with the outcome variable. However, there's also substantial correlations among the predictors themselves. That is, they overlap.
Some variance in job satisfaction accounted by a predictor may also be accounted for by some other predictor. If so, this other predictor may not contribute uniquely to our prediction.
There's different approaches towards finding the right selection of predictors. One of those is adding all predictors one-by-one to the regression equation. Since we've 5 predictors, this will result in 5 models. So let's navigate to and fill out the dialog as shown below.
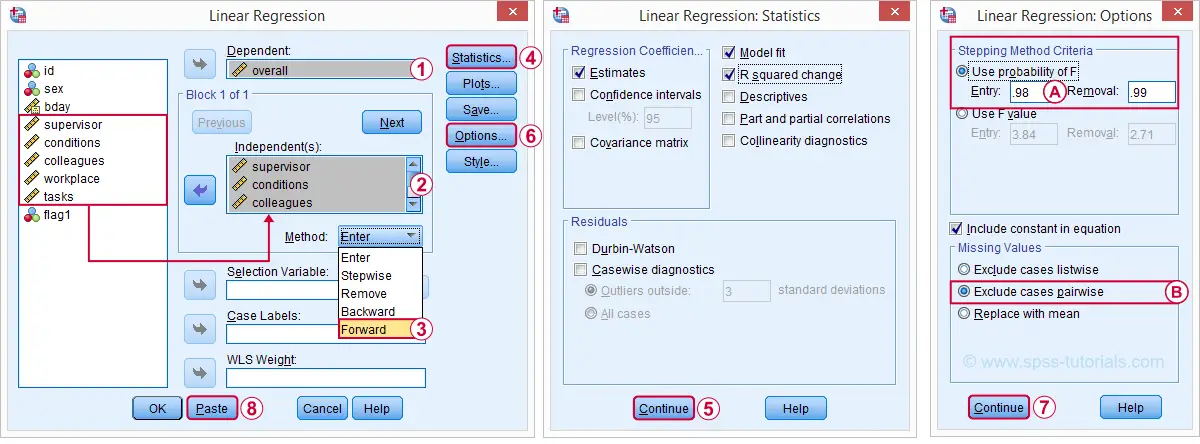
 The method we chose means that SPSS will add all predictors (one at the time) whose p-valuesPrecisely, this is the p-value for the null hypothesis that the population b-coefficient is zero for this predictor. are less than some chosen constant, usually 0.05.
The method we chose means that SPSS will add all predictors (one at the time) whose p-valuesPrecisely, this is the p-value for the null hypothesis that the population b-coefficient is zero for this predictor. are less than some chosen constant, usually 0.05.
 Choosing 0.98 -or even higher- usually results in all predictors being added to the regression equation.
Choosing 0.98 -or even higher- usually results in all predictors being added to the regression equation.
 By default, SPSS uses only cases without missing values on the predictors and the outcome variable (“listwise exclusion”). If missing values are scattered over variables, this may result in little data actually being used for the analysis. For cases with missing values, pairwise exclusion tries to use all non missing values for the analysis.Pairwise deletion is not uncontroversial and may occasionally result in computational problems.
By default, SPSS uses only cases without missing values on the predictors and the outcome variable (“listwise exclusion”). If missing values are scattered over variables, this may result in little data actually being used for the analysis. For cases with missing values, pairwise exclusion tries to use all non missing values for the analysis.Pairwise deletion is not uncontroversial and may occasionally result in computational problems.
Syntax Regression I - Model Selection
REGRESSION
/MISSING PAIRWISE /*... because LISTWISE uses only complete cases...*/
/STATISTICS COEFF OUTS R ANOVA CHANGE
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=FORWARD supervisor conditions colleagues workplace tasks.
Results Regression I - Model Summary
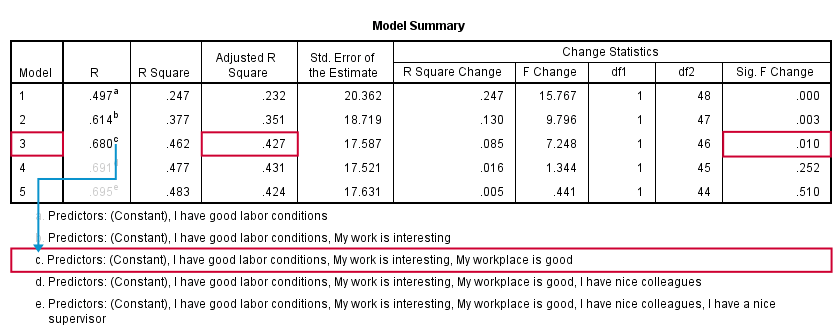
SPSS fitted 5 regression models by adding one predictor at the time. The model summary table shows some statistics for each model. The adjusted r-square column shows that it increases from 0.351 to 0.427 by adding a third predictor.
However, r-square adjusted hardly increases any further by adding a fourth predictor and it even decreases when we enter a fifth predictor. There's no point in including more than 3 predictors in or model. The “Sig. F Change” column confirms this: the increase in r-square from adding a third predictor is statistically significant, F(1,46) = 7.25, p = 0.010. Adding a fourth predictor does not significantly improve r-square any further. In short: this table suggests we should choose model 3.
Results Regression I - B Coefficients
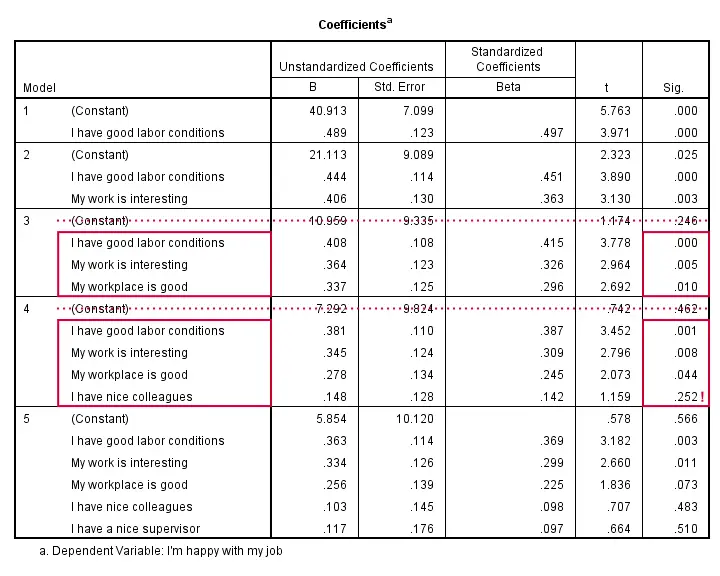
The coefficients table shows that all b-coefficients for model 3 are statistically significant. For a fourth predictor, p = 0.252. Its b-coefficient of 0.148 is not statistically significant. That is, it may well be zero in our population. Realistically, we can't take b = 0.148 seriously. We should not use it for predicting job satisfaction. It's not unlikely to deteriorate -rather than improve- predictive accuracy except for this tiny sample of N = 50.
Note that all b-coefficients shrink as we add more predictors. If we include 5 predictors (model 5), only 2 are statistically significant. The b-coefficients become unreliable if we estimate too many of them.
A rule of thumb is that we need 15 observations for each predictor. With N = 50, we should not include more than 3 predictors and the coefficients table shows exactly that. Conclusion? We settle for model 3 which says that
Satisfaction’ = 10.96 + 0.41 * conditions
+ 0.36 * interesting + 0.34 * workplace.
Now, before we report this model, we should take a close look if our regression assumptions are met. We usually do so by inspecting regression residual plots.
Regression II - Residual Plots
Let's reopen our regression dialog. An easy way is to use the dialog recall ![]() tool on our toolbar. Since model 3 excludes supervisor and colleagues, we'll remove them from the model as shown below.
tool on our toolbar. Since model 3 excludes supervisor and colleagues, we'll remove them from the model as shown below.
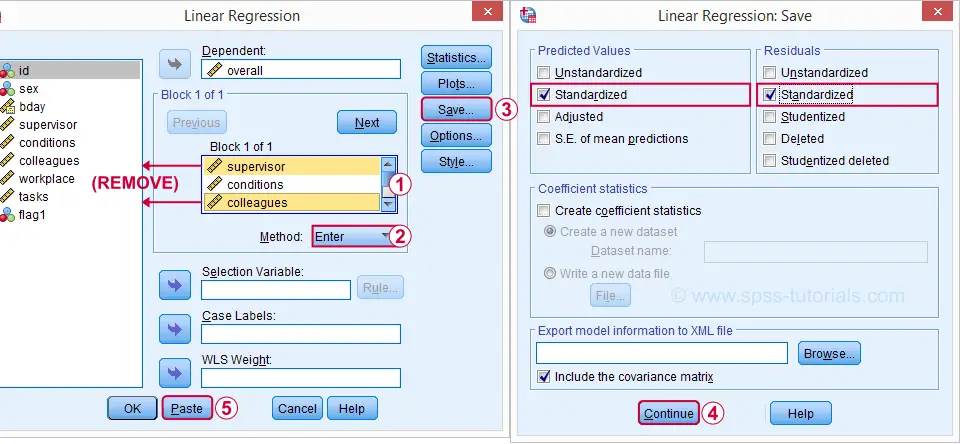
Now, the regression dialogs can create some residual plots but I rather do this myself. This is fairly easy if we  save the predicted values and residuals as new variables in our data.
save the predicted values and residuals as new variables in our data.
Syntax Regression II - Residual Plots
REGRESSION
/MISSING PAIRWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA CHANGE /*CI(95) = 95% confidence intervals for B coefficients.*
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=ENTER conditions workplace tasks /*Only 3 predictors now.*
/SAVE ZPRED ZRESID.
Results Regression II - Normality Assumption
First note that SPSS added two new variables to our data: ZPR_1 holds z-scores for our predicted values. ZRE_1 are standardized residuals.
Let's first see if the residuals are normally distributed. We'll do so with a quick histogram.
frequencies zre_1
/format notable
/histogram normal.
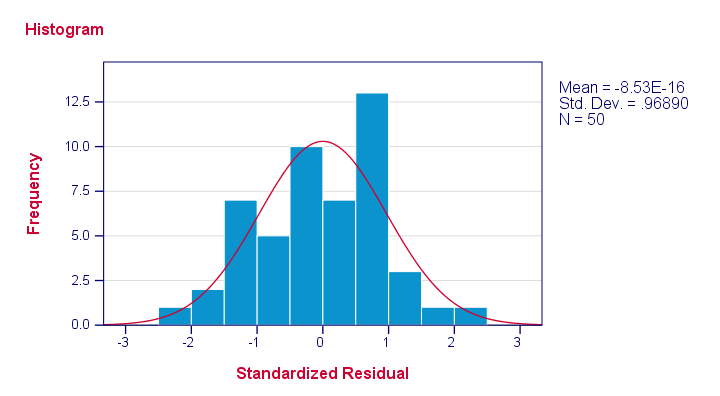
Note that our residuals are roughly normally distributed.
Results Regression II - Linearity and Homoscedasticity
Let's now see to what extent homoscedasticity holds. We'll create a scatterplot for our predicted values (x-axis) with residuals (y-axis).
GRAPH
/SCATTERPLOT(BIVAR)= zpr_1 WITH zre_1
/title "Scatterplot for evaluating homoscedasticity and linearity".
Result
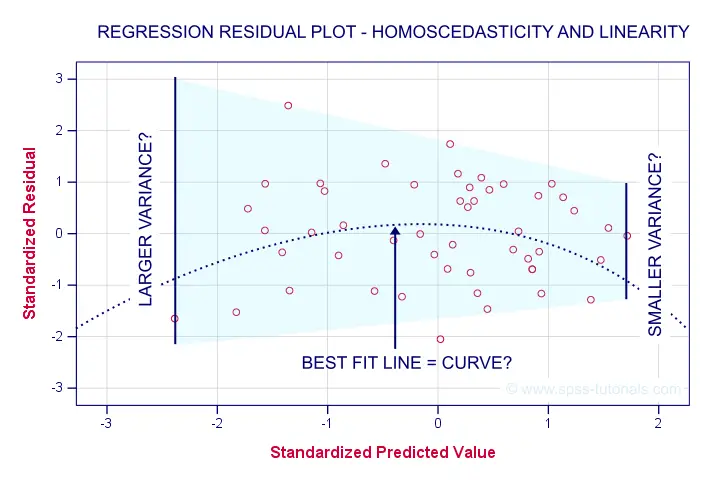
First off, our dots seem to be less dispersed vertically as we move from left to right. That is: the residual variance seems to decrease with higher predicted values. This pattern is known as heteroscedasticity and suggests a (slight) violation of the homoscedasticity assumption.
Second, our dots seem to follow a somewhat curved -rather than straight or linear- pattern. It may be wise to try and fit some curvilinear models to these data but let's leave that for another day.
Right, that should do for now. Some guidelines on APA reporting multiple regression results are discussed in Linear Regression in SPSS - A Simple Example.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS

THIS TUTORIAL HAS 20 COMMENTS:
By Ashoka Ekanayake on April 9th, 2021
Thank you for great support to understand analysis.
By Dr. Batool on May 30th, 2021
i need some help
By Marian Hista Villacrusis on July 4th, 2021
This is helpful in current study. Thanks for helping me understand the perks of interpreting data!
By ALI on January 19th, 2022
Hi all
, have not had a chance to read through yet .
looks great and enriching.
will get back with comment.
thanks again
its great
By Olumide on May 15th, 2022
These concepts are too technical. Is there no way to explain SPSS usage to a newbie?